边有两种类型，一种是machine arc（也叫disjunctive arc），由同一机器上的前一道工序指向相邻的后一道工序。图中彩线部分表示machine arc。另一种是job arc（也叫conjunction arc），由同一工件上的前一道工序指向相邻的后一道工序。图中黑色实现部分代表job arc。两种边分别表示machine 和job的两个约束，因此一个点最多引申出4条边。

除此之外，图中还有两个超级源点，起始点和终止点（图中的0号start和10号finish）。他们是虚拟的点，代表加工开始和结束。Start点只有job arc，分别连向每个工件的第一道工序；Finish 点也只有job arc，从每个工件的最后一道工序连接到此点。（要注意边的顺序！）

图中的边上没有权值，权值存放在点上，代表加工时间。起始、终止点加工时间为0。

读到这里大家应该能感受到，一幅图实际上已经代表了一个解。点（即工序）的加工开始、结束时间都可以通过最长路算法得出。整个schedule的最大makespan（加工时间）就是起始点到终止点的最长路距离。如果这幅图里没有环，则解可行；否则为不可行解。

这里的最长路又称为critical path（关键路径），即图中粉色框框起的部分。

最长路的算法小编没有找到很好的资料，自以为可以用DFS写，如果在邻域算子后要进行全部工件starting time的更新，那么可以使用bellman－ford算法，这些在小编的代码里都有实现。

结论：很多JSP、FJSP论文的tabu search都是基于析取图进行的，因为可以使用图的特性，毕竟容易操作。

k－insertion

相较于JSP，小编能查到的FJSP的邻域较少，这一部分主要参考一篇2000年的论文 “Effective neighbourhood functions for the fexible job shop problem”，讲解其中的k－insertion邻域。

k－insertion其实就是一个insert操作，简单来说就是将critical path中的每一个操作，分别插入到其他可加工机器的某个位置，形成新解。这里强调，无论什么邻域搜索，一定要在critical path上做文章，才容易改变解的makespan。

实际上，并不是一个机器上的所有位置都需要插入的。如果一道工序由于job边约束，加工时间在考前的位置，那么插入某台机器靠后的位置显然不会使加工时间缩短。考虑到这一点，我们只需要挑出可能使结果更优的位置，执行插入操作。

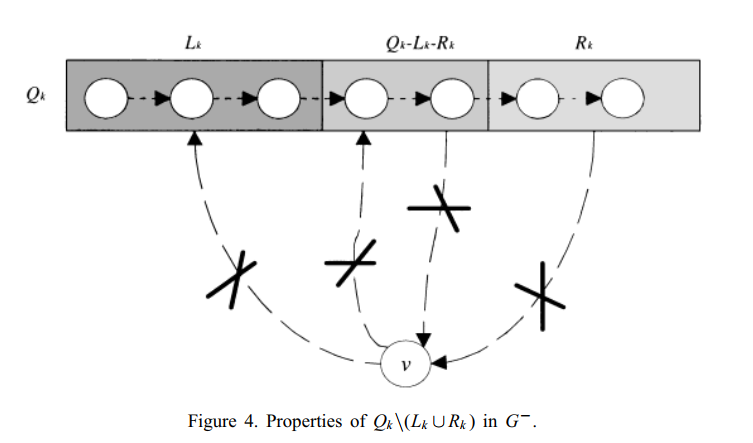
论文中对每个机器上的工序根据starting time（开始加工的时间）进行排序，然后根据公式计算出两个边界：L＿k， R＿k。再通过二分查找找到这两个位置。经过证明，只有两者的并集（图中中间的部分）插入后可能优化结果。这里的计算公式需要定义一些新变量，难度不大但是不好讲清，想要深入研究的同学可以下载代码、论文进一步研究，这里暂时不多说了。

前面我们反复强调，我们的tabu是要嵌入到每一个个体中的，因此计算速度一定要快。如果对TS的每一个解都精确运算出makespan，速度会很慢（第一个tabu就是这样的）。因此，我们需要特殊的估值方法。

论文中的估值是一个上界。只需要根据前文定义的一些变量进行简单的加减乘除运算即可得出，极大优化了时间复杂度。这里同样不多解释。

然而，在实现析取图的k－insertion后，小编发现自己实现的速度依旧很慢，嵌入个体后算法根本跑不动。因此小编尝试了一下GA和TS的并行操作，用GA的初始解进行TS操作，发现结果却是有优化，但是时间还是太久。小编目前也找不到代码资料，只能自行编写，因此陷入瓶颈。有了解这块的同学可以和小编进一步交流！

这里再提一句，JSP、FJSP的tabu禁忌表可以用插入或交换前后的的位置，制作一个二维表来表示，用单纯的解作为禁忌对象会拖慢速度。

结论：Tabu2效果不错，但是可能是因为析取图部分没有写好，时间容易爆炸。